Theorie

0. Astronomische Grundlagen

0.1. Grössen und Richtungen

0.1.1. Astronomische Einheit

Da die Entfernungen zwischen den Astronomischen Körpern (Planeten, Monde,etc.) sehr gross sind,
hat man sich in der Astronomie darauf geeinigt Entfernungen in Astronomische Einheiten (AE)
anzugeben. Eine AE ist der mittlere Abstand zwischen Erde und Sonne, also ca. 149.597.870 km.

0.1.2. Ekliptik

Die Erde dreht sich um die Sonne und bewegt sich dabei auf einer elliptischen Flugbahn.
Diese Flugbahn befindet sich auf einer Ebene, Ekliptikebene genannt.
Für fast alle Berechnungen am Sonnensystem dient die Ekpliptik als Referenzebene.
Auf Bild 0.1 ist diese Ebene durch ein Gitter dargestellt, bei welchem eine
Gittermasche exakt eine Astronomische Einheit (AE) breit und lang ist.
Als X-Achse der Ebene wurde die Achse zum Frühlingspunkt und als y-Achse die
rechtwinklige Richtung dazu gewählt.

Bild 0.1 Definition der Ekliptikebene

0.1.3. Frühlingspunkt

Zu einem bestimmten Zeitpunkt im Jahr bildet der Mittelpunkt der Erde und der Mittelpunkt der
Sonne eine Gerade, die auch durch die Äquatorebene der Erde geht.
Somit stellt diese Gerade die Schnittgerade der Äquatorebene zur Bahnebene (Ekliptik) dar.
Dieser Moment, an dem das zutrifft passiert z.Z. ca. am 21.03. weswegen er Frühlingspunkt
genannt wird (engl. vernal equinox)
In diesem Moment scheint die Sonne exakt senkrecht auf einen Punkt des Äquators.
In weiterer Verlängerung zeigt die Gerade, quasi hinter der Sonne, z.Z. zum Sternzeichen Widder (engl. Aries).
In der Antike (vor ca. 2500 Jahren) zeigte die Gerade zum Stenzeichen der Fische.
Der exakte Moment verschiebt sich infolge der Erdpräzission von Jahr zu Jahr um ca. 5 Stunden.
Im Jahr 2025 war er am 20.03. um 9:01 UTC. Diese Richtung ändert sich also nur sehr langsam im laufe der Jahrhunderte
und wird deshalb bei allen astronomischen Berechnungen als Referenzachse (X-Achse) benutzt.

Bild 0.2 Definition des Frülingspunkts

0.1.4. heliozentrisches Koordinatensystem

Wie der name schon andeutet, wird beim heliozentrischen Koordiantensystem (hKOS) die
Sonne (griechisch Helios) in den Koordiantenursprung gelegt.
Weiterhin nimmt man die Gerade die zum Frühlingspunkt zeigt (s.0.1.3.) als X-Achse,
die Y-Achse setzt man um 90 grad zur X-Achse verstetzt auf der Ekliptik-Ebene liegend
Die Z-Achse ist wieder um 90 grad zur Y-Achse versetzt, sodass alle drei Achse der
Rechte-Hand-Regel entsprechend ein dreidimensionales Koordiantensystem bilden.

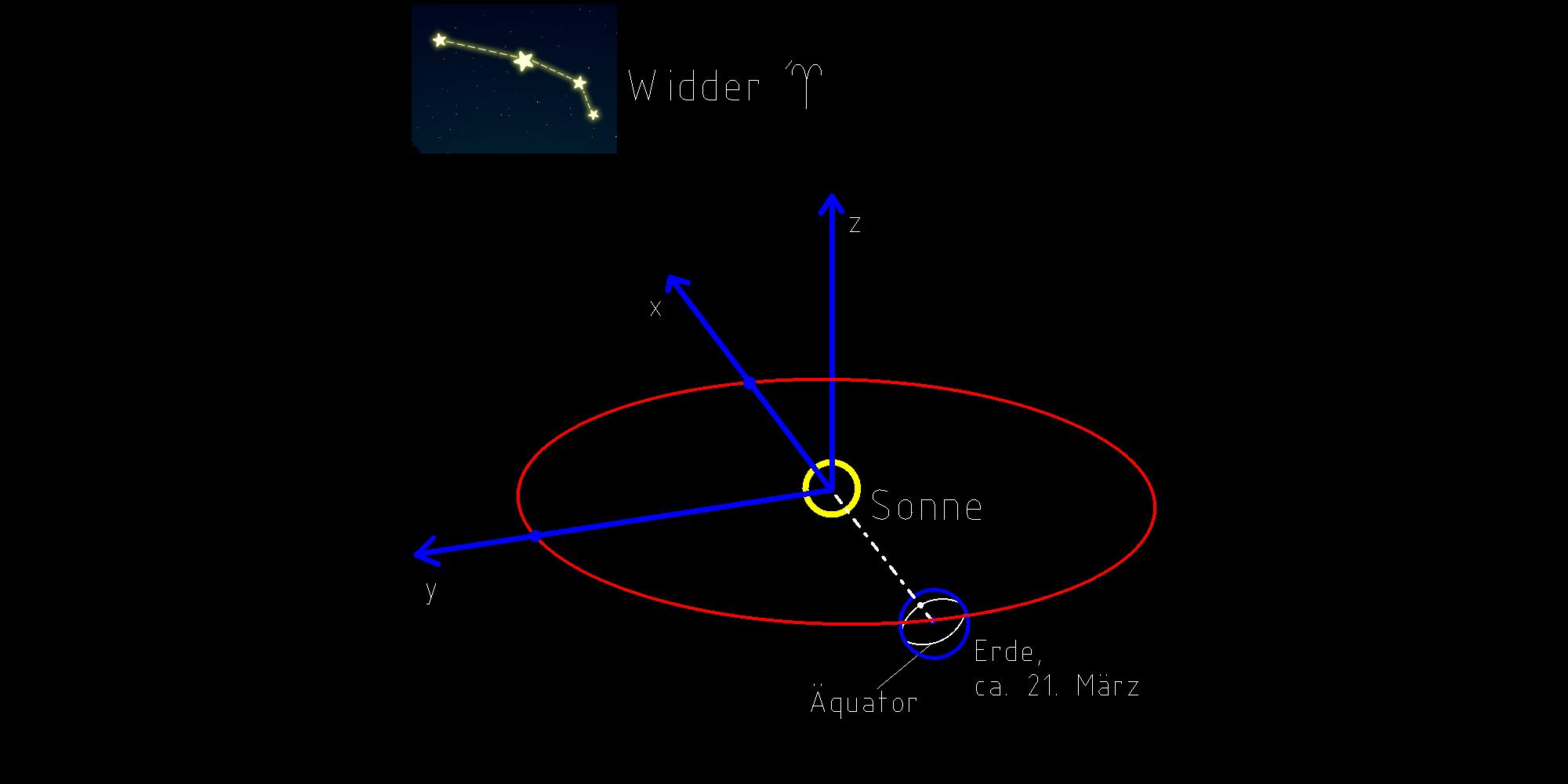
Bild 0.2 Definition des heliozentrischen Koordiantensystems

0.1.5. geozentrisches Koordiantensystem

Anders als beim heliozentrischen Koordiantensystem liegt bei diesem die Erde im
Koordiantenursprung. Weiterhin ist dessen X-Achse ein Gerade beginnend vom Mittelpunkt
der Erde zum Frühlingspunkt, die X-Achse wird um 9o grad versetzt auf die Ekliptik gelegt
die Z-Achse liegt dann wieder um 90 grad versetzt und bildet mit den zwei anderen ein
dreidimensionales Koordiantensystem nach der Rechte-Hand-Regel.
Das geozentrische Koordiantensystem (gKOS) wird oft als Refeferenzsystem verwendet
bei der Bahnberechnung von Erdsatelliten.

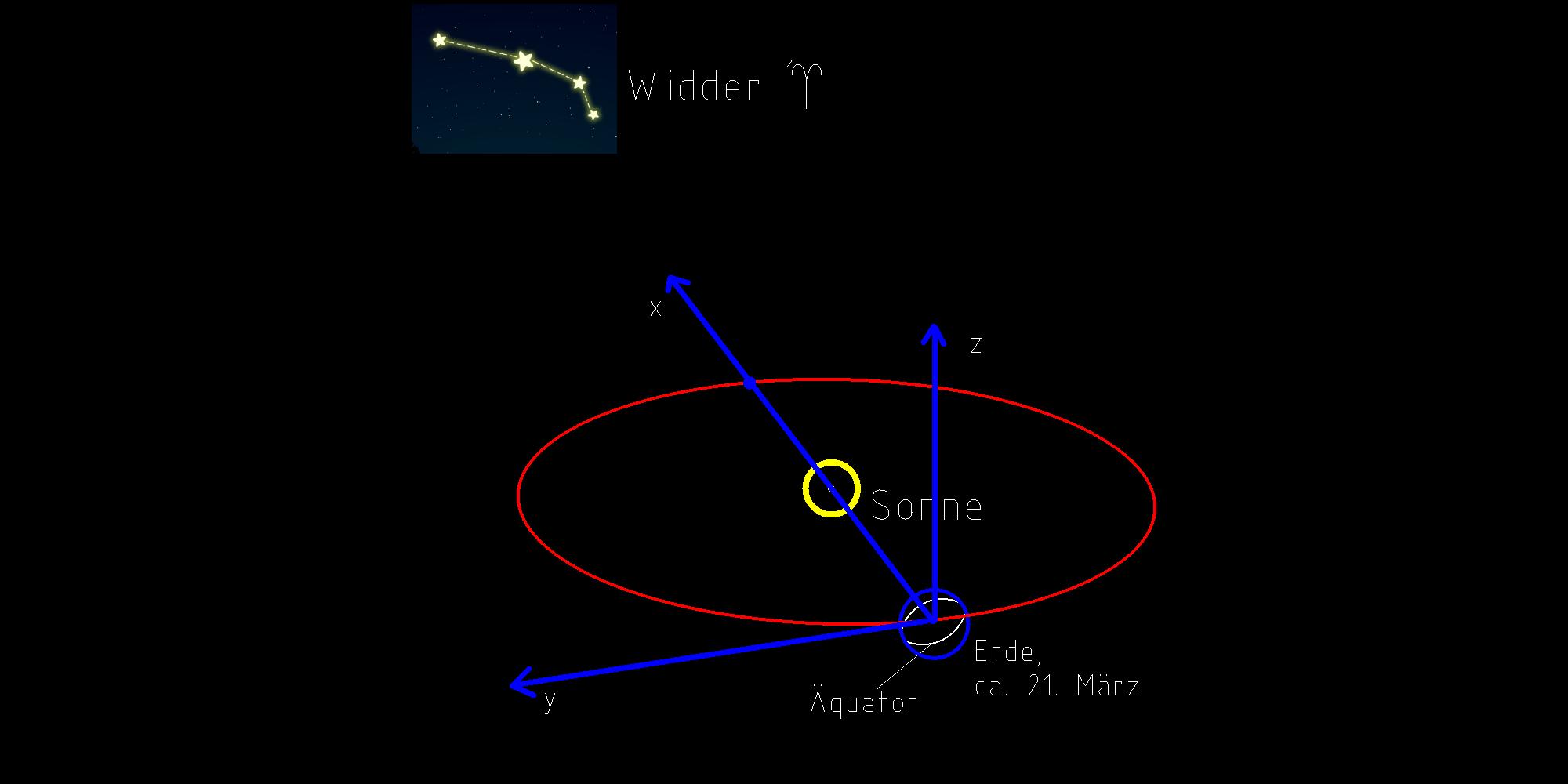
Bild 0.3 Definition des geozentrischen Koordiantensystems

0.1.6. topozentrisches Koordiantensystem

Beim topozentrischen Koordiantensystem wird der Koordiantenursprung auf ein Punkt
auf der Oberfläche der Erde gelegt. Meist dient dieses System dazu die Winkel (Azimut und Elevation)
zu bestimmten, mit denen man vom Standpunkt des Betrachhters zu einen Objekt am Himmel kommen kann.

1. Ellipsenorbitale nach Johannes Kepler

1.0. Mathematische Definition der Ellipse

Bild 1.0 Mathematische Definition einer Ellipse

a: grosse Halbachse einer Ellipse
b: kleine Hablachse einer Ellipse
F1,F2 : Brennpunkte einer Ellipse, Ort der grossen umkreisten Masse
O: Mittelpunkt der Ellipse
e: Exzentrizität der Ellipse

Interaktiv:

a :

b :

e :

1.1. Definition des Orbits als Ellipsenbahn

Bild 1.1 Ellipsenbahnebene in Bezug auf Referenzebene, aus [5]

M: Mittelpunkt der Bahnellipse ( = O bei anderen Grafiken)
P: Perihel (Bahnnächster Punkt an grosse Masse im Brennpunkt)
Ω: Longitude des aufsteigenden Knoten (Winkel zw. Frühlingspunkt und aufsteigenden Knoten)
ω: Argument des Perihels (Winkel zw. Aufsteigenden Konten und Perigäum)
P: Perihel (nahester Punkt im Orbit an schwere Masse)
ϒ: Referenz-Richtung des Frühlingspunkt (Sternzeichen Widder)
i: Inklination, Winkel zw. Bahnebene und Referenzebene

1.1.4. Form und Grösse des Orbits

Die Form und Grösse des Orbits wird wie schon in 1.0. durch zwei Parameter festgelegt:

1.1.4. Lage des Orbits

Die Lage des Orbits in Bezug auf den Schwerpunkt wird festgelegt durch:

1.2. Position des Objekts auf dem Orbit

will man die exakte Position des Objekts im Orbit bestimmen,
fehlt noch der Winkel zwischen dem Perigäum und und dem Objekt,
auch wahre Anomalie genannt (ν)

Bild 1.2 Mathematische Darstellung einer Ellipsenbahn in Bezug auf eine Referenzebene [2]

N’-N: Schnittgerade mit Ekliptik
N: aufsteigender Schnittpunkt
N’: absteigender Schnittpunkt
M: Zentralgestirn im Ellipsenschwerpunkt (grosse Masse M, z.B. Sonne)
x: Richtung Frühlingspunkt (FP)
Ω: Winkel zw FP und N
ω: Winkel zw. N und P
ν: wahre Anomalie
i: Inklination der Bahnebene in Bezug zur Referenzebene
m: Position des Objektes (kleine Masse, z.B. Planet)

kennt man die Laufzeit T, die das Objekt für ein vollständigen Umlauf benötigt
und weiss wo das Objekt zu einem bestimmten Zeitpunkt t₀ seine Position hatte (M₀),
so lässt sich ein theoretischen Umlauf auf einer Kreisbahn mit Radius a vorstellen.
(s. grüner Kreis in Abb. 1.3)
Nimmt man den Zeitunterschied (Δt) zu t₀,
lässt sich der Winkel auf dieser theoretischen Kreisbahn bestimmen.
Diesen nemnnt man die Mittlere Anomalie M.
In zeitlicher Abhängigkeit zur verstrichenen Zeit Δt erhält man M(Δt):

M(Δt) = M₀ + Δt * 360° / T

aus der Mittleren Anomalie lässt dann sich die Kepler-Gleichung für
die Exzentrische Anomalie E(t) aufstellen zu :

E(t) = M(t) + e * sin(E(t))

Diese transzendentale Gleichung lässt sich ein durch Iterationsverfahren lösen:

E₀ = M₀
E₁ = M₀ + e * sin(E₀)
E₂ = M₀ + e * sin(E₁)
...
bis E_n+1 - E_n kleiner als die notwendige Genauigkeit

Mit dem so berechneten E erhält man die wahre Anomalie ν zu:

tan \frac{ν}{2} = tan \frac{E}{2} * \sqrt{\frac{1+e}{1-e}}

Bild 1.3 Definition der Parameter der Ellipsenbahn

M: Grosse Masse (z.B Sonne oder Planet)
m: kleiner Masse (z.B.Planet oder Satelit)
a: grosse Halbachse der Ellipse
b: kleine Halbachse der Ellipse
P: Perihel (nahester Punkt des Orbits an grosser Masse)
A: Aphel (fernster Punkt des Orbits an grosse Masse)
ν: wahre Anomalie (winkel zw. Perihel und orbitalen Objekt)
E: exzentrische Anomalie (Winkel zw. Orbitmittelpunkt und orbitalen Objekt)
x: Position des orbitalen Objekts auf dem Orbit
x’: Position des orbitalen Objekts auf einem Hilfskreis mit Radius a